复合闭路定理
柯西积分定理在多连通区域
实质上也是解析区域向包含奇点的区域(不解析)的推广
闭路变形原理
闭路变形原理
在区域内的一个解析函数沿闭曲线的积分,不因闭曲线在区域内作连续变形而改变它的值
只是要求被积函数为解析函数,但是区域可以有奇点
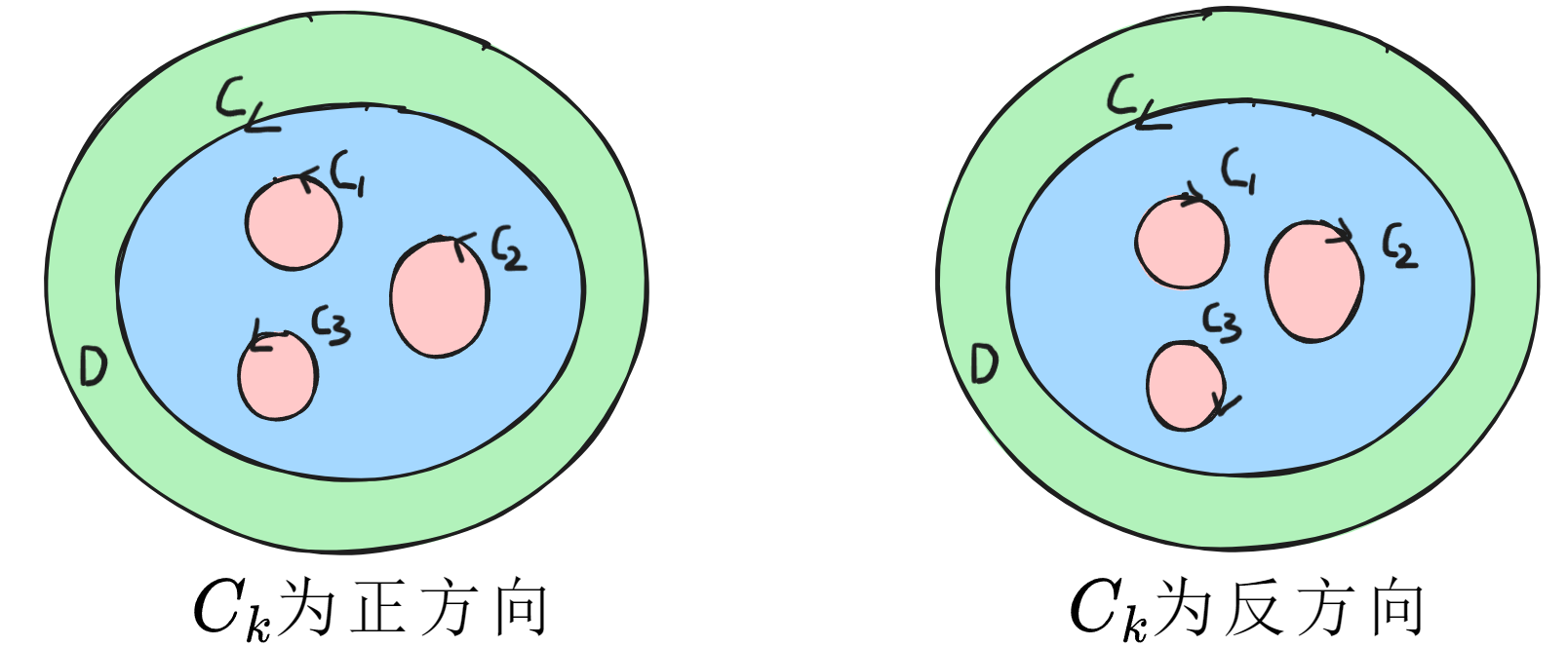
复合闭路定理
均取正方向
按逆时针(正方向), 顺时针(反方向)
应用
结合复积分得到的重要性质,使得应用非常简单
?
柯西积分定理在多连通区域
实质上也是解析区域向包含奇点的区域(不解析)的推广
闭路变形原理
在区域内的一个解析函数沿闭曲线的积分,不因闭曲线在区域内作连续变形而改变它的值
只是要求被积函数为解析函数,但是区域可以有奇点

结合复积分得到的重要性质,使得应用非常简单
?